Prelab / BLE

Using 'ble_arduino.ino' as the framework, I can just modify the loop and add the case I need to complete the task of BLE control.
In this lab, I add two cases:
1. LAB_6: Execute PID control over a fixed amount of time (15s), making the cart approach the wall quickly and stop 300mm away from the wall and storing the data into an array of fixed size (1000*3) in the meantime.
2. GET_DATA: Write the data into 'tx_characteristic_string' sequentially, so that the PC can get the data of the car running through notify function in Jupyter Lab.

        case GET_DATA:
            
            for(i = 0; i < last_i; i++){
              tx_estring_value.clear();
              tx_estring_value.append(" ");
              tx_estring_value.append(data[i][0]); //time
              tx_estring_value.append(" ");
              tx_estring_value.append(data[i][1]); //distance
              tx_estring_value.append(" ");
              tx_estring_value.append(data[i][2]); //duty cycle
              tx_characteristic_string.writeValue(tx_estring_value.c_str());
            }
            
            break;

The car will store the data during operation in an array including time, distance from the wall, and duty cycle. After operation, I first activate a notify function in Jupyter Lab and than send the 'GET_DATA' command to the Artemis Board. Then I can get all the data needed.

Task A: Don’t Hit the Wall

First, I define the error to be 'distance - setpoint' and then implement the PID control.

        get_tof();
        err = dis - set_point;

For P, it's just a parameter proportional to error:

        P = K_p * err;
        if(P > P_max) P = P_max;
        else if(P < -P_max) P = -P_max;

For I, it's the integral of error over time. Since we can't subdivide time infinitely, I initialize integration to 0 and keep accumulating error*d_t to get an approximation. Then I make the integration back to 0 when the car pass the set_point so that it won't continue pushing the car away from the set_point.
I use it as a positive feedback mechanism to mitigate speed reduction when the car is getting closer to the set_point so that it can keep a relatively higher speed when crossing the set_point.

        if(err * pre_err < 0) integ = 0;
        integ += err * d_t / 1000;
        I = K_i * integ;
        if(I > I_max) I = I_max;
        else if(I < -I_max) I = -I_max;

For D, it's the differential of error which is the speed of the car in a broad sense. I use it as a negative feedback mechanism that only triggers when the car is moving away from the setpoint, providing an inverse factor to the PID.

        dif = (float)(err-pre_err)/d_t*1000;
        if(dif * err <= 0) D = 0;
        else D = K_d * dif;

I set a cap for both P and I but not for D because when D is in effect, it reduces the speed, which also reduces D itself.
Finally, calculate the duty cycle using PID and deadband:

        raw = P + I + D;
        
        //Deadband
        if(err>0) org = deadband;
        else if(err == 0) org = 0;
        else org = -deadband;

        //calculate speed
        dc = org + raw;

Overall, P is the dominant factor, which decreases linearly with decreasing error. I is a factor that assists P, which can keep the car at a relatively higher speed when it is constantly approaching the set_point. D is a negative feedback factor for sudden braking after crossing the set_point.
So K_p should be relatively larger and K_i next. K_d can be large because the speed decreases rapidly so that D becomes small rapidly.

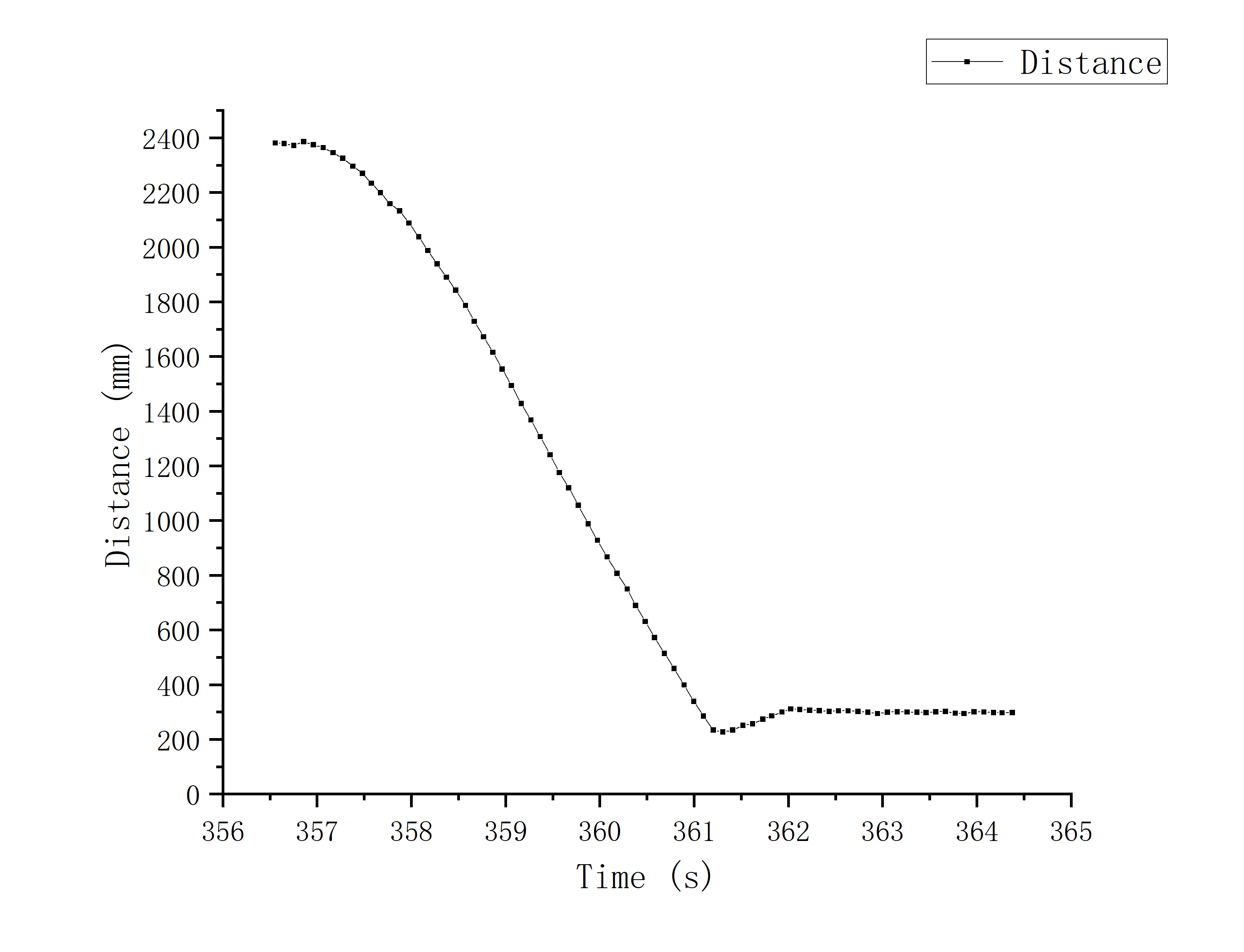
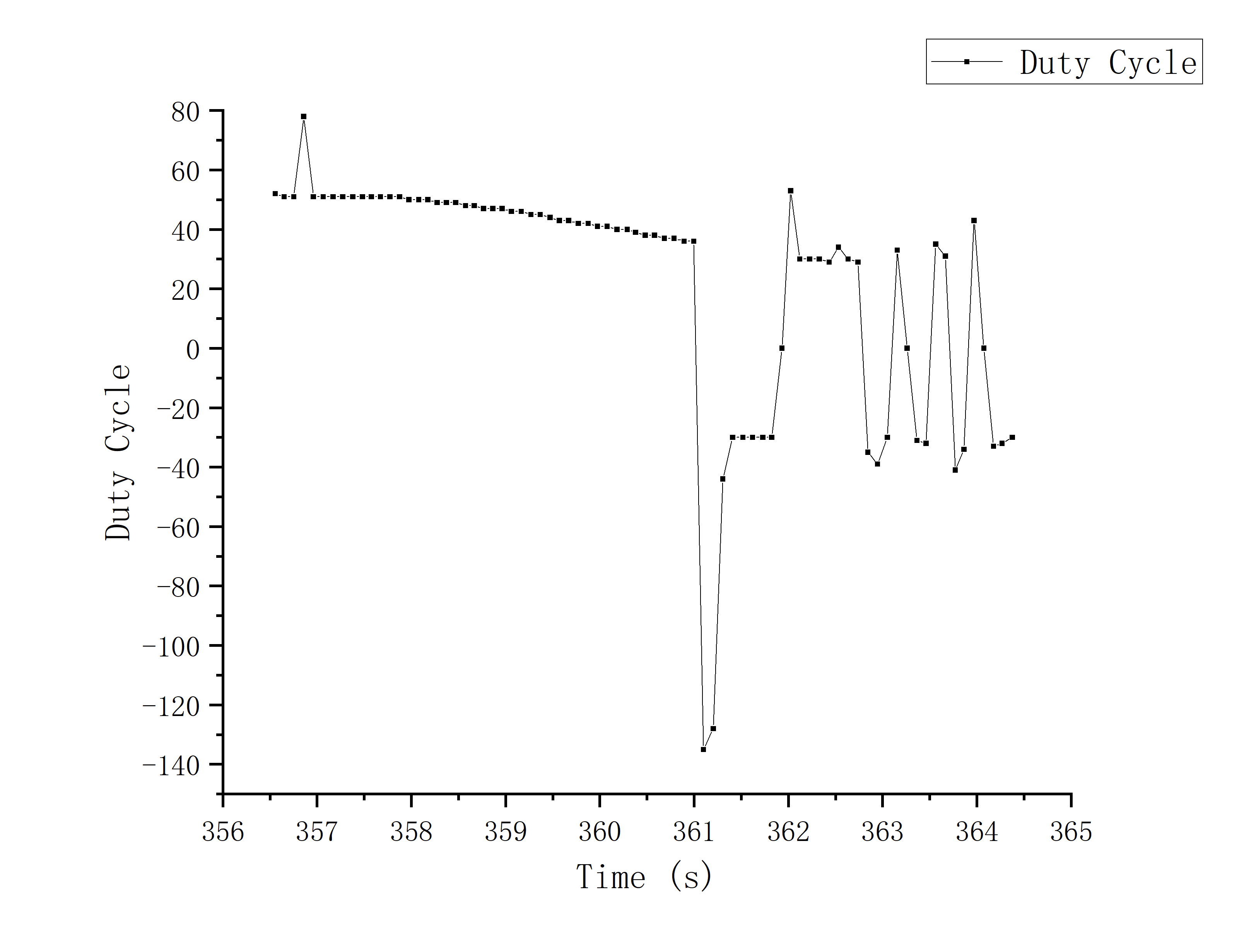
K_p = 0.01; K_i = 0.001; K_d = 0.2; Deadband = 30;

K_p = 0.02; K_i = 0.003; K_d = 0.2; Deadband = 30;

Some other demo videos which support for reliability:

K_p = 0.01; K_i = 0.001; K_d = 0.2; Deadband = 30;

K_p = 0.02; K_i = 0.003; K_d = 0.2; Deadband = 30;

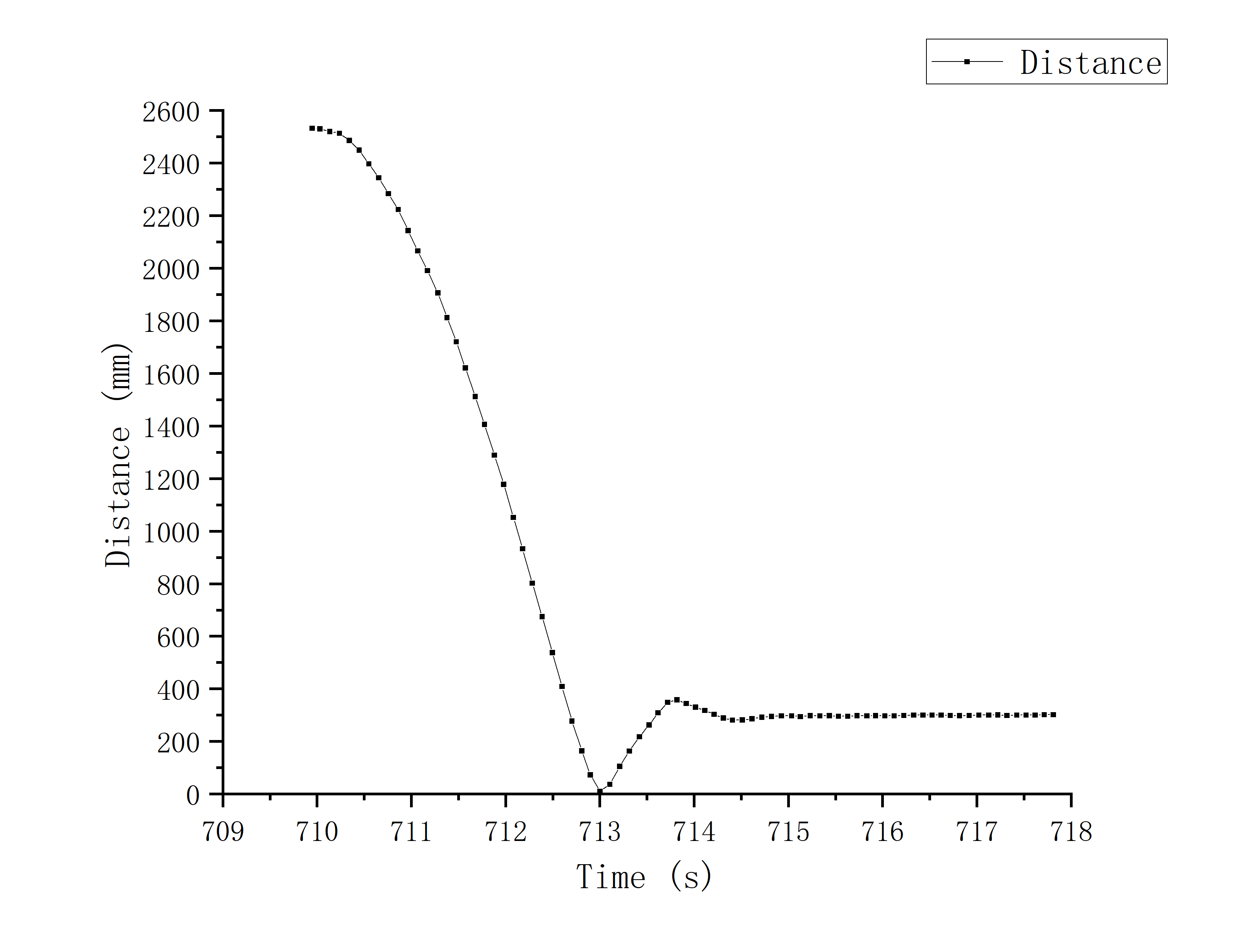
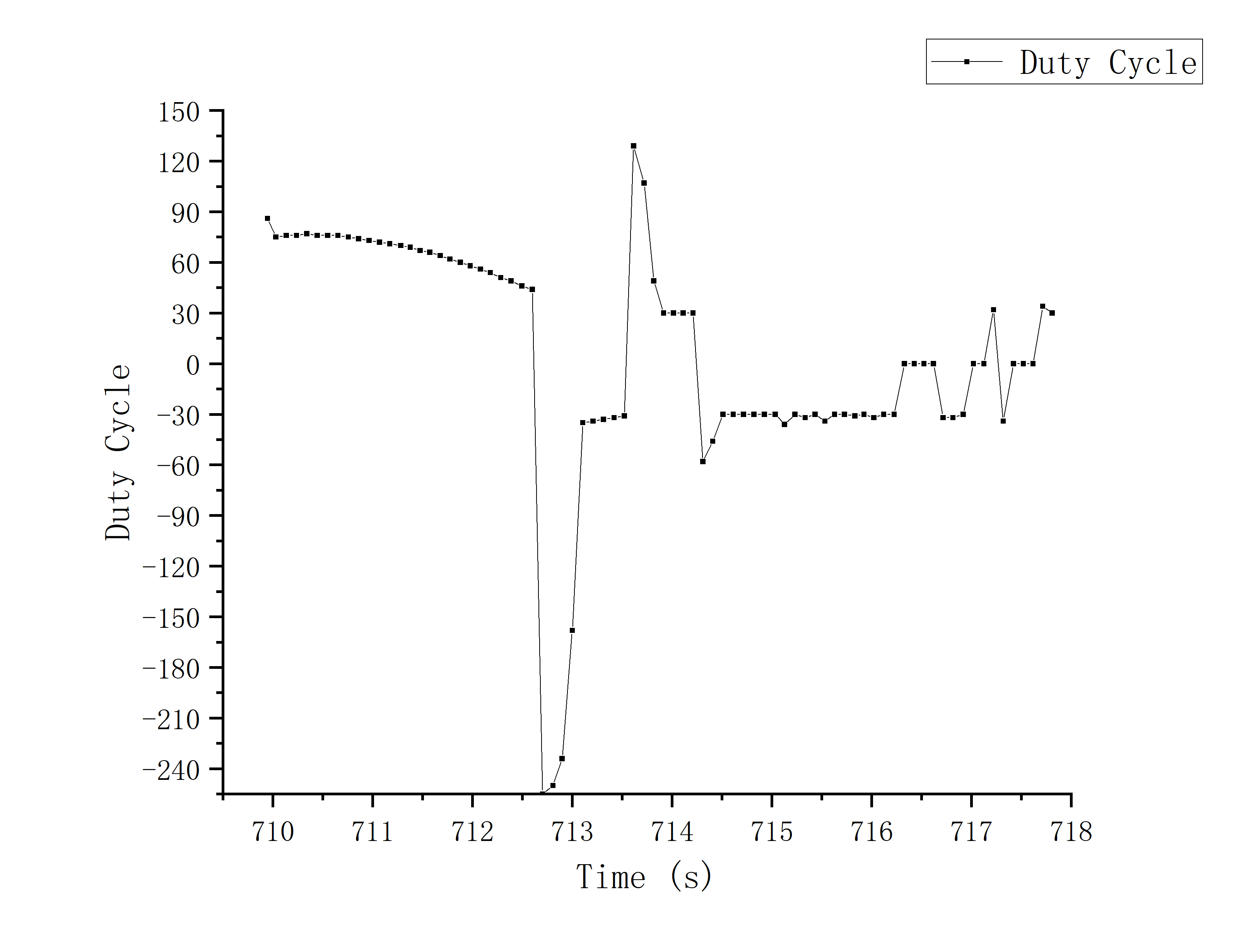
We can see an instantaneously large reverse value in both of the graphs of duty cycle, which means the car wanted to make a sudden brake when crossing the set_point to avoid crashing into the wall. And this is the functionality of differential part of my design.
However, due to the limitation of ToF sampling frequency (~100ms once), it will crash into the wall when the car's passing speed is fast enough.

Discussions

The frequency of one loop is limited by the sensor sampling rate of ToF whose period is about 100ms.
Therefore, when the speed of the car is relatively fast and the set_point is close to the wall, the car cannot brake in time after passing the set_point and will hit the wall.

I set a cap for the integrator and make it to be 0 when the car pass the set_point so that it would not affect the car catastrophically

In my design, the derivative is used to brake the car effectively and it will decrease rapidly so I may not need an LPF for this Time

First, if the derivative is not initialized properly, it will start the car at an unpredictable high speed. So So I initialize it carefully before every boot.
Second, I just take use of the Derivative kick to brake the car efficiently.

For the convenience of parameter adjustment, I set up a case to help change several commonly used values such as K_p, K_i, K_d, set_point, etc. This way I can constantly modify the run parameters by sending command to the Artemis Board via BLE control.