Objective

The goal of this lab is to have the robot navigate through a set of waypoints in that environment as quickly and accurately as possible.

Methods

For this task, I thought of two relatively feasible solutions:
1. Make the car complete the route through precise PID control without the help of localization
2. Get the position of the robot by localization first, then calculate the relative distance and angle to the next waypoint, and finally move the robot via PID control

The most important point of this method is the accuracy. Theoretically, we can first calculate the relative distance and angle between each two waypoints, and then make the robot to the next waypoint by PID control if the accuracy of each step can be guaranteed.

This method is a theoretically more reliable one. Before action, put all the waypoints into the system for initialization. First get the position of the robot by localization in LAB 12 (using both prediction step & update step or only update step). Then calculate the relative distance and angle between belief and the next waypoint. Finally, make the robot to the next waypoint by PID control.

My choice

Although method 2 seems more reliable, it is much more prone to many difficult problems in practical experiments.
In LAB 12, we can easily find that due to the large error of the ToF readings in the case of long distances and the deviation of the angle during the 360 degree turn, the localization of the robot may have a huge offset that cannot be ignored. And once there is a large error in localization, the calculated relative distance and angle between belief and the next waypoint will also be greatly affected, making the robot move in a completely wrong direction and target distance.
In addition, method 2 also takes a long time to complete the localization, and needs to be relocalized when the positioning error is large, which further increases the required time and violates our original intention to complete the route as fast and accurate as possible.

Therefore, I choose method 1: step-by-step PID control. And there are three very important points of the method to note:
1. Make sure the robot doesn't deviate from the route when moving in a straight line
2. Ensure a precise turning angle of the robot
3. Accurately measure the relative distance and angle between every two waypoints

Preparation

Due to the uneven ground, different friction of the wheels on both sides, different voltages and currents on motor drivers, and the different starting time of motor drivers, etc., the robot is very prone to deviate from the track when moving forward.
In order to solve this problem, it is not enough to use only factor to adjust the duty cycle input into the motor drivers. Because this factor may change under different input, battery level and ground factors, it may still cause the robot to deviate from the straight line.

Therefore, I integrate the control of the IMU sensor in LAB 9 to the initial PID control in LAB 6, which can help the robot monitor in real time whether the angle it faces has changed via gyroscope.
This method allows the robot to monitor the change of the angle in real time while moving forward while maintaining its angle change to 0 through another PID control (that is, the direction of movement remains unchanged).
Since the sampling rate of the gyroscope is much higher than the ToF sensor (about 25 times the sampling rate of the ToF), I modified the function to get the ToF readings so that it will not pause the robot's program while ranging data. When ToF has not obtained new data, the program will use the original data as its distance (same as LAB 6), and continue to monitor and correct the rotation angle of the robot when running forward via gyroscope.

        void get_tof_con(){
            if(state == 0){
                //Write configuration bytes to initiate measurement
                distanceSensor.startRanging(); 
                state = 1;
            }
            else if(distanceSensor.checkForDataReady()){
                //Get the result of the measurement from the sensor
                dis = distanceSensor.getDistance(); 
                distanceSensor.clearInterrupt();
                distanceSensor.stopRanging();
                state = 0;
            }
        }

Since the program simulates the integration of acceleration over time by multiplying the angular velocity by time to calculate robot's angle, the higher the sampling frequency (that is, the shorter the single sampling time), the more accurate the angle can be obtained.
To this end, I change the fixed waiting time (based on if statement) in the function of getting the gyroscope reading to a trigger-based wait (using a while loop to ensure that it updates as soon as the gyroscope gets the new data).

        void get_IMU(){
            while(!myICM.dataReady()){
                delay(1);
            }
            myICM.getAGMT();
        }

Since the route is known, we can obtain the distance between any two waypoints by precise theoretical calculation. However, in the actual test, the placement of the robot, the position of the ToF, and the measurement error of the ToF may cause the actual required displacement distance to deviate from the theoretical calculation value.
To ensure the correctness of the data input into the robot, I manually placed the robot to each waypoint and take its ToF readings (take 20 measurements using ToF for each waypoint and use the sample with smaller variance to calculate the average as the distance) to calculate the distance between consequent two waypoints.

Since the robot needs to adjust the direction while moving forward, this means that the rotation speed of the wheels on both sides is different, which also means that the duty cycle input to the motor drivers that controls the wheels on both sides is different.
Since two sets of independent PID controls are used in the control process, two duty cycles that control forward (dc_tof) and steering (dc_yaw) respectively will be generated. So I combined the two control signals through a function so that the robot can continuously adjust its direction as it moves forward, keeping the direction.

        void gostraight(){
            //left wheel
            if(dc_tof+dc_yaw>maxspeed){
                analogWrite(A2, 0);
                analogWrite(A3, maxspeed);
            }
            else if(dc_tof+dc_yaw>=0){
                analogWrite(A2, 0);
                analogWrite(A3, dc_tof+dc_yaw);
            }
            else if(dc_tof+dc_yaw<-maxspeed){
                analogWrite(A2, maxspeed);
                analogWrite(A3, 0);
            }
            else{
                analogWrite(A2, -(dc_tof+dc_yaw));
                analogWrite(A3, 0);
            }
            //right wheel
            if(dc_tof-dc_yaw>maxspeed){
                analogWrite(A0, maxspeed*fac);
                analogWrite(A1, 0);
            }
            else if(dc_tof-dc_yaw>=0){
                analogWrite(A0, (dc_tof-dc_yaw)*fac);
                analogWrite(A1, 0);
            }
            else if(dc_tof-dc_yaw<-maxspeed){
                analogWrite(A0, 0);
                analogWrite(A1, maxspeed*fac);
            }
            else{
                analogWrite(A0, 0);
                analogWrite(A1, -(dc_tof-dc_yaw)*fac);
            }
        }

Implementation

After the above steps, we can get a route with detailed information in a map (The scale in the figure may deviate due to the difference between the actual measured value and the theoretical value):

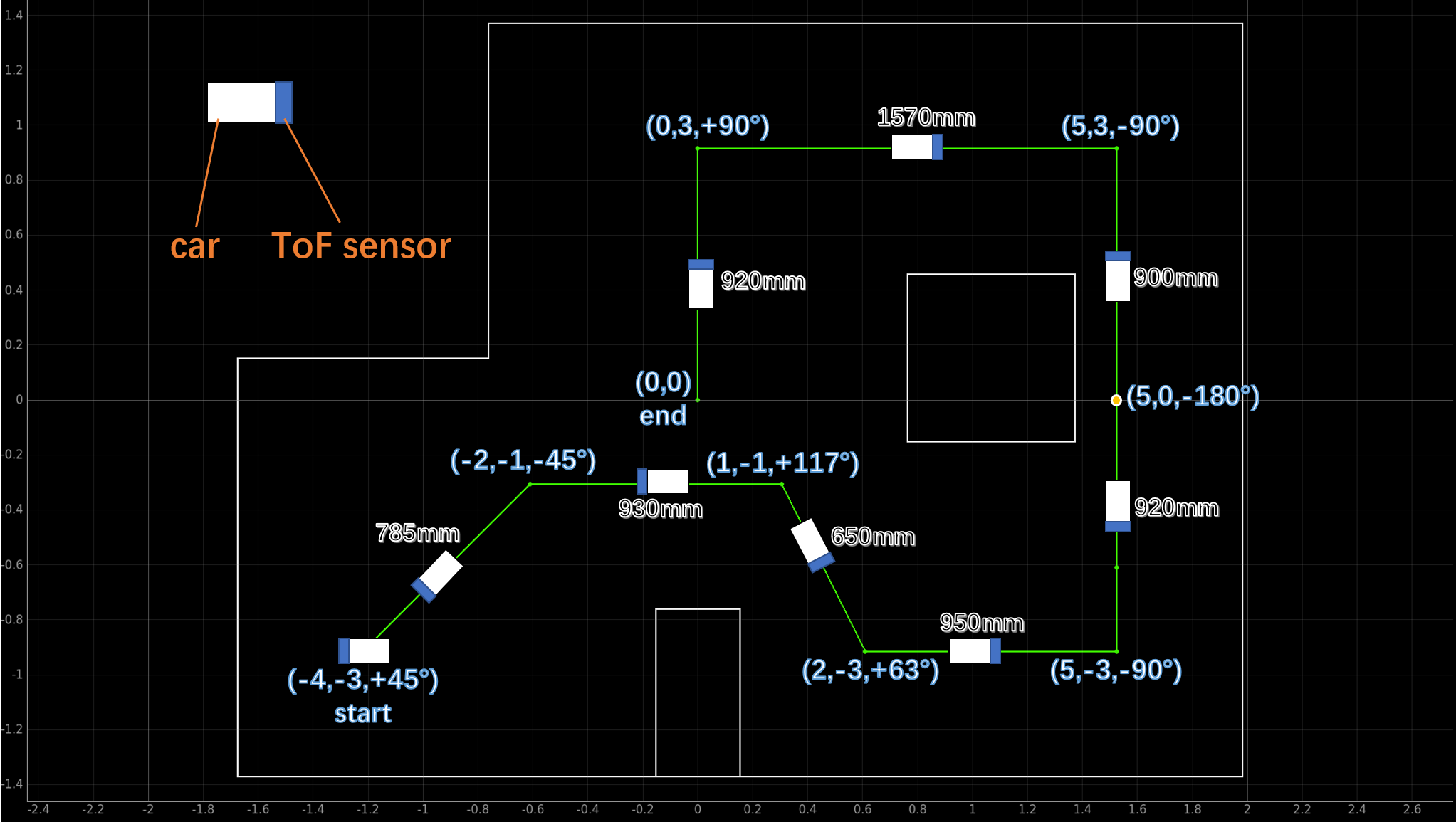
The map above shows the rotation angle of the robot at each waypoint (counterclockwise rotation is the positive direction) and the driving distance between each consecutive two waypoints.

It is not difficult to find from the map that I always make the ToF sensor face the wall with a closer distance during the operation, and when encountering a longer distance movement (from (5,-3) to (5,3)), I let the robot do a 180 degree turn at its midpoint (5,0) to change the orientation of the ToF sensor so that it still faces the the wall at a shorter distance.
This is because I found in the experiment that when the distance detected by the ToF sensor is getting longer and longer, its readings fluctuate more and more seriously, which directly affects the accuracy of navigation.

In this lab, I use BLE communication to send commands to the robot from the computer for control. The commands used mainly include the following three:
1. DEFAULT_SET: Set the ratio of the duty cycle of the two motor drivers (fac), the upper limit of the duty cycle of the motor drivers (maxspeed), and the initial angle of the robot (yaw_agre)
3. SET_GOAL: Set the target distance to move forward (set_dis), the direction (set_yaw), and time (timelimit)
3. TURN: Turn the robot to the target angle in place
4. GO_STRAIGHT: Make the robot move the set distance and turn its angle to the set angle

Then I implemented the entire navigation through the combination of the above commands. I just run all the selected cells at once in Jupyter Lab so that I can follow the robot for video recording.

Due to the internal settings of BLE communication, the robot will not accept the next command until the current command is completed. Only after the robot completes the current command and sends the completion signal to the computer, the computer will send the next command to the robot. Therefore, even if I run all the cells at one time, the computer will automatically wait for the robot to complete the current command before sending the next command with no command loss.
In addition, breaking the whole navigation into multiple cells can make the debugging process easier.

Below is a good demo video:

Below are some not that good demo videos:

Discussion

Navigating with the help of Bayes filter is definitely an ideal way. It can predict and update the position of the robot in motion, and then generate appropriate commands for the robot by calculating the relative distance and angle between current belief and the next waypoint.
However, due to the increase in operations, a series of problems also arise:
1. Similar to lab11, the prediction step will be very inaccurate due to sensor reading errors and model calculation biases
2. The update step includes a 360 degree turn to collect data, which takes a long time to ensure its correctness and stability
3. The update step needs a lot more rotation during the navigation, which can seriously increase the deviation of the angle without an absolute direction as a reference, causing the calculated route to deviate, making the robot more prone to hit obstacles
4. If the belief obtained by Bayes filter at any waypoint differs greatly from ground truth, then the calculated command will make the robot move in a completely wrong direction and distance, making the entire navigation fail. Only by ensuring that each localization is very accurate, the robot can complete the navigation, which is obviously very difficult (we all know from LAB 12 that localization at some waypoints is very unreliable)

Step-by-step PID control greatly reduces the operations during the navigation process and reduces the angle offset as much as possible. The process is simple as the user only needs to calculate all the route information and send it to the robot, which is easy to operate.
However, since the essence of this method is to let the robot perform a fixed process, it does not have the ability to automatically correct after the deviation of the route. In addition, this method requires extremely high precision in the operation of the robot, including accurate rotation angle and running distance.

In this lab, the most difficult and problem-prone process is the angular offset during the rotation process, for both methods.
Assuming that in method 1, the localization process is always very accurate (that is, the calculated position is always consistent with the ground truth), after completing the update step (a 360 degree turn), the angle offset can still cause a wrong calculated state (the robot thinks it is rotated 360 degrees when it is not). Since there is no signal transmitting device on the waypoints, the robot cannot correct its direction without outside help, which will cause the route to completely deviate from the plan when the error gradually expands.
This also troubles method 2 as it's an open loop. The accumulated angular deviation will cause the robot to gradually deviate from the planned route and potentially hit obstacles during subsequent navigation.

To solve this problem, there are the following feasible measures:
1. Improve the sampling rate and accuracy of the gyroscope to reduce the angle deviation as much as possible
2. Correct the direction of the robot in real time by detecting external signals. For example, use the magnetometer to detect the direction of the geomagnetic field as an absolute reference direction, or set a magnetic field generator at the waypoint to obtain the relative angle from the robot.